（参考）　　アキノ氏の反重力理論と実験結果の概略　　　　　　　（2008 １１/１５　　追加）



　　ブラジルのアキノ（Ｆｕｒａｎ ｄｅ Ａｑｕｉｎｏ）教授・Maranhao State University　らによる、重力をゼロにするシステム・・・”Ｓｙｓｔｅｍ　Ｇ”は有名である。それは媒質（鉄粉）に埋め込まれた銅製のダイポールアンテナを円形に曲げ交流電流を流して電磁波を供給することによって、ある電流値（約１３０Ａ）で突然そのドーナツ部分の重量が０になる、という驚くべきものである。

　　また、アキノ氏によるこの現象に関する理論が発表され、基本的には特殊相対性理論の範囲内（＋電磁波の輻射理論等）で議論されている。彼の理論によると、慣性質量ｍｉ と重力質量ｍｇ とは一般相対性理論の「等価原理」が成り立たないものとして、電磁波の輻射（放射）が無いときにのみそれらが等しくなり、電磁波が輻射されている場合は重力質量が慣性質量よりも小さくなり、その減少量は流す超低周波（ＥＬＦ）電流の電流値の２乗程度できいてくるというものである。

　　ただし、報告されている実験のパラメータには一部不明な部分があり、彼の実験過程の詳細な写真はあるが、重量の著しい減少の実験結果についてはグラフのみで写真やビデオなどが無く、理論付けも正しいかどうかはなんとも言えない。因みに、”零点エネルギー”等の量子力学的説明は理論の基礎的部分には用いられないで、単純な特殊相対論のみである。
　　（＊　特殊相対性理論は間違いやすいものの典型であるので、要注意）
　　このように割合単純な理論で重力を制御することができるということが今まで報告されなかった背景には、実験した人があまりいなかったためと考えられる。（あるいは狂言か？）

　　以下、理論の基本的部分の概略と”Ｓｙｓｔｅｍ Ｇ”の実験結果の一部をまとめた。

　　（参考ＨＰ）　　Professor Fran De Aquino's Webpage、　　　about the examinations of the- System G -（2002）・・・　詳細な実験過程、
　　　　　　　　　　Mathematical Foundations of the Relativistic Theory of Quantum Gravity（2008）・・・　アキノ氏の”重力理論”
　　　　　　　　　　フリーエネルギーと反重力の研究会の中にアキノ氏の和訳有り
　　　　　　　　　　　　　　　　　　　　　　　　・・・・・・　ただし、理論も実験結果も間違っている可能性が大きいので注意

　　（１）　重力質量 ｍ_ｇ と 慣性質量 ｍ_ｉ との関係式：


　　等価原理が成立しないことに基づき、次のパラメータを区別する。

　　重力質量： ｍ_ｇ 、　慣性質量： ｍ_ｉ　、　慣性静止質量： ｍ_ｉ0 、　
　　重力エネルギー： Ｅ_ｇ 、　慣性エネルギー： Ｅ_ｉ 、　重力静止エネルギー： Ｅ_ｇ0 、　慣性静止エネルギー： Ｅ_ｉ0 、慣性力学エネルギー： Ｅ_ｉｋ　


　　自由粒子について、その運動は、ラグランジアン　　を用いて　　より、
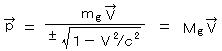　　　　　　　　　　　　・・・・　（１）　　　　のように、重力質量　ｍ_ｇ を用いて表わされる。

　　また、その力は　　Ｆ_ｉ ＝ ｄｐ^→ /ｄｔ　より、　　　、　
　　運動エネルギーは　　Ｅ_ｇ ＝ ｐ^→・Ｖ^→ − Ｌ　より、　　　　　　・・・・　（２）
となる。　この運動エネルギーを変形して、
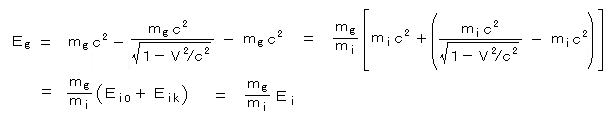　　・・・・　（３）

のように、重力エネルギーＥ_ｇ、慣性エネルギーＥ_ｉ、　ｍ_ｇ、ｍ_ｉ　の関係が導かれる。

　　この力学的慣性エネルギー Ｅ_ｉ は、　　　　（ｍ_ｉ0： 静止慣性質量）　　　　・・・・　（４）　　
　　（速度が光速に比べて充分遅い場合（Ｖ＜＜ｃ）、　　　　で近似され非相対論となる。）



　　一方、エネルギー保存則より、　　　であり、重力エネルギーの減少は慣性エネルギーの増加に対応している。

　　それゆえ、 Ｅ_ｉ に対する �凾d_ｉ は、Ｅ_ｇ に対する �凾d_ｇ ＝ −�凾d_ｉ となり、さらに、

　　 Ｅ_ｉ ＝ Ｅ_ｉ0 ＋ �凾d_ｉ 、　Ｅ_ｇ ＝ Ｅ_ｇ0 ＋ �凾d_ｇ ＝ Ｅ_ｇ0 −�凾d_ｉ 、　したがって、　Ｅ_ｇ ＋ Ｅ_ｉ ＝ Ｅ_ｇ0 ＋ Ｅ_ｉ0 　となる。

　　（２）と（４）を比較して、　　が得られ、これは　 Ｅ_ｉ ＝ Ｅ_ｉ0 ＋ Ｅ_ｉｋ　より、　　Ｅ_ｇ ＝ Ｅ_ｉ0 − Ｅ_ｉｋ　となる。

　　したがって、　この最後の２式を引き算すると、　　　　　　・・・・　（５）
が得られる。


　　重力エネルギーと重力質量と運動量との間には、次のような関係がある。
　　（１）と（３）を比較して、　　　　　　　　　　　・・・・　（６）
　　このハミルトニアンは、　　　　　　　　　　・・・・　（７）

　　同様に、慣性エネルギーと慣性質量について、
　　　　　　　　　　　　　　　　　　　　　　　　・・・・　（８）
となる。（ 一般相対性理論でｍ₀ （静止質量）の場合、（８）は”アインシュタインの関係式”と同じ）

　　また、（５）をハミルトニアンで書き換えると、　　　　　　　・・・・　（９）

　　ここで、�凾g_ｉ　は�凾垂ﾅ表わされ、　　

　　したがって、ｐ ＝ ０ 、すなわち、初期の運動が０の場合、
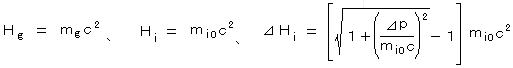　　　となって、これらを（９）に代入して、

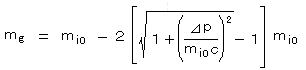　　　　　　　　　　　　　　　　　　　　　　　　　　・・・・・　（１０）

が得られる。（＊　　質量減少分を強調するため、右辺第２項はこのような表記になっている）
　　この（１０）式は、運動量の増加 �凾� が、一定の慣性静止質量 ｍ_ｉ0 に対して、重力質量 ｍ_ｇ を減少させることを表わしている。
　　したがって、�凾� ＞ （√５/２）Ｍ_ｉ0 ｃ　のとき、重力質量 ｍ_ｇ は 負になる！？





　　（２）　電磁輻射による重力質量減少の理論：


　　（１０）式における 粒子の�凾� を増加させる方法として、　�@　ローレンツ力、および、　�A　電磁輻射 による、２つの方法が存在する。

　　ローレンツ力は、通常、次のように書くことができる。
　　　　　　　　　　　　　　
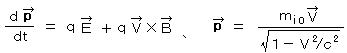
　　一方、（１）より、　　　　だから、　　　
　　したがって、
　　　　　　　　　　　　　　　　　　　
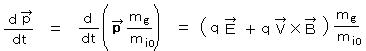
となり、これがローレンツ力の一般的な表現となる。


　　輻射の場合は、次のように �凾� を表わすことができる。

　　音波を含む一般的な輻射の場合、粒子は、輻射圧 ｄＰ を、単位体積　ｄＶ ＝ ｄｘｄｙｄｚ　の 単位面積 ｄＡ に受け、輻射エネルギー ｄＵ を吸収する。
　　このときの 輻射速度（放射の媒質内の伝播速度）を ｖ とすると、 ｄｚ ＝ ｖｄｔ　となる。すなわち、放射圧は、
　　　　　　　　　　　　　　　　　　　・・・・　（１１）
　　ｄＤ ＝ ｄＵ/ｄｔｄＡ ＝ Ｐ/ｄＡ： （単位面積あたりの輻射パワー（工率）、輻射パワー密度）

　　この単位面積に働く力は、 ｄＦ ＝ ｄＰｄＡ　だから、　ｄＦ・ｄｔ ＝ ｄＵ / ｖ　となり、　ｄＦ ＝ ｄｐ/ｄｔ　より、　　ｄｐ ＝ ｄＵ/ ｖ　　これを積分して、
　　　　　　　　　　　


　　また特に、電磁波の放射の場合、その伝播速度 ｖ は、　波数ベクトル ｋ^→ 、ｌｋｌ ＝ ｋ_ｒ ＋ ｉｋ_ｉ ； ε、　ε_ｒ 、 μ_ｒ 、 σ　をそれぞれ、電磁波が伝わる媒質の誘電率、比誘電率、比透磁率、導電率 とすると、
　　　　　　　　　　　　・・・・　（１２）
　　ゆえに、屈折率 ｎ_ｒ は、
　　　　　　　　　　　　　　　　　　・・・・　（１３）
　　したがって、 �凾� は、（１１）より、　　　　　　　となり、　この �凾� を （１０）式に代入すると、
　　電磁波輻射による重力質量減少の式、
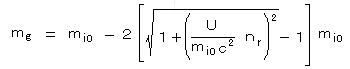　　　　　　　　　　　　　　　　　・・・・　（１４）

が得られる。（Ｕ： 輻射エネルギー）

　　この（１４）式に、具体的な装置の諸元の数値を代入すれば、重力質量の減少量を見積ることができる。





　　（３）　電磁波輻射実験（System G）とその結果：


　　ω（＝２πｆ） ＜＜ σ/ε　（電磁波の周波数 ｆ が充分低い）の場合、（１４）式は簡略化され、　ε ＝ ε_ｒε₀、　ｃ² ＝ １/（ε₀μ₀）　より、
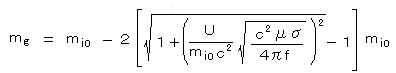　　　　　　　　　　　　　　　　　　・・・・・　（１５）
となる。
　　ただし、電磁波が伝わる媒質についての、　透磁率： μ ＝ μ_ｒ・μ₀ （μ₀ ＝ ４π×１０^-7（Ｈ/ｍ））、電気伝導度： σ（Ｓ/ｍ）、とする。


　　ダイポール・アンテナから、この導電性と磁性を併せ持つ媒質（・・・鉄粉を押し固めたもの）に輻射される 電磁波の強度 Ｐ は、
　　２Ｌ＜＜λ　（電磁波の波長よりもアンテナ長がはるかに短い）の場合、　Ｌ： アンテナ長、　Ｉ₀： 印加する正弦波電流のピーク値、　として、
　　　　　　　　　　　　　　


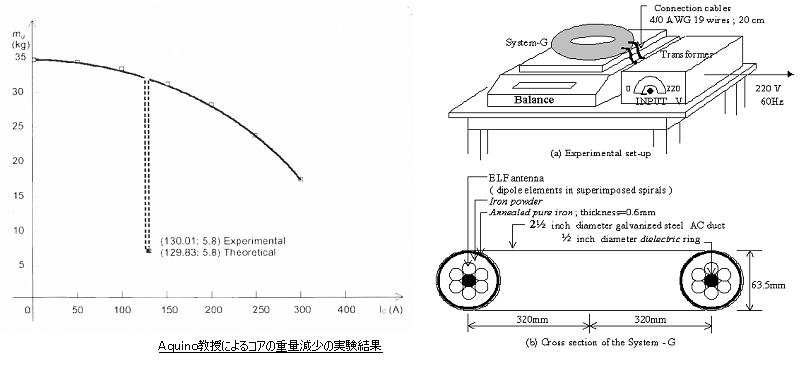
　　アンテナを平行に円形に巻き、媒質として鉄粉を充填したドーナツに超低周波（ＥＬＦ）電流を印加する実験をする。（これが、アキノ氏の”System G”）

　　輻射エネルギー Ｕ は、　Ｓａ： 原子の幾何学的断面積、　Ｓ： 外壁（外側のアニール純鉄ドーナツ）曲面の面積、　伝達効率： η、　として、（ω＜＜σ/ε より近似して）
　　　　　　　　　　　　　　

　　アンテナの長さ Ｌ： １２（ｍ） （＝６（ｍ）＋６（ｍ）を反平行・円形にそれぞれ３ターン巻く）、　押し固めた鉄粉の比透磁率 μ_ｒ： 約７５、　押し固めた鉄粉の導電率 σ： 約１０（Ｓ/ｍ）であり、　ドーナツ外側はアニール（純鉄板をアニール（焼鈍）し軟磁性化）純鉄シールド（μｒ： ２５０００、σ’： １．０３×１０⁷（Ｓ/ｍ）、ｔ＝０．６ｍｍ）で覆い、電磁波を内側に全反射させる。
　　また、ドーナツ内部の全重量 ｍ_ｉ0： ３５（ｋｇ）、　外側のアニール純鉄ドーナツ曲面の面積 Ｓ： ０．３７４（ｍ²）、　印加する超低周波電流の周波数 ｆ： ６０（Ｈｚ）、　伝達効率 η： １、　とする。
　　ここで、鉄粉内の電磁波の伝達速度 ｖ は、（１２）式より、　ｖ ＝ ｃ/（√（μ_ｒσ/（４πｆε₀）） ＝ ８９５（ｍ/Ｓ） （屈折率 ｎ_ｒ ＝ ３．３５２×１０⁵）となる。

　　以上のデータから、（１５）式 右辺・かぎ括弧・ルート内の（括弧）²の数値のオーダーを見積ると、
　　　　　　　　

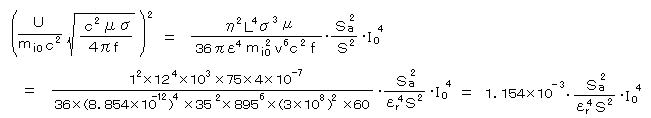
　　ここで、文献におけるいくつかのパラメータ（ 鉄原子の幾何学的断面積 Ｓ_ａ、　 Ｄ ＝ Ｐ_ａ/Ｓ_ａ ＝ Ｐ/Ｓ、　押し固めた鉄粉の比誘電率 ε_ｒ　）が不明なため、計算はここまでであるが、アキノ氏の計算結果では（１５）式は次のようになる。
　　　　　　　　　　　　　　　　　　　　　　　・・・・　（１６）

　　したがって、ドーナツ内の鉄粉が完全に重量を失う　ｍ_ｇ ＝ ０　となる印加電流値 Ｉ₀ は、　Ａ ＝ ４．４×１０-9　とおいて、（１６）より、

　　　　　　　　　０　＝　１　−　２（√（１＋Ａ・Ｉ₀⁴）　−　１）　、　　　∴　Ｉ₀　＝　（５/（４Ａ））^1/4　≒　１２９．８（Ａ）　　程度となる。



　　”System G”の実験装置では、電源装置（可変電流型の手巻きのトランス： １次コイルφ４．１１５ｍｍ１２ターン、２２０Ｖ、　２次コイル１/２インチ銅棒、２ターン、　インピーダンス：　入力４．２Ω、出力＜１ｍΩ）も作成し、銅線のダイポール・アンテナを下図のように円形に巻いて、周りに鉄粉（粒度１５０μｍ以下のかなり細かいもの）を充填・プレスし、アニール純鉄板で外側をシールドしている。

　　実験結果では、バネ秤で上から吊るされた約３５ｋｇのドーナツ部分の重量が、交流電流（６０Ｈｚ）の増加と共に徐々に減少し、約１３０（Ａ）で、突然０にまで減少し、この電流値が計算結果とほぼ一致していると報告している。（・・・　この写真、あるいは、ビデオ等は無い）

　　

　　＊　また、気体プラズマ（蛍光灯の水銀プラズマ、アメリシウム２４１による空気プラズマ）による重力遮蔽の新しい理論が報告されているが、実験結果は無い。　これも、上記の理論と同じ原理であり、プラズマの導電性がきいているので、周波数が０−１ｍ（ミリ）Ｈｚと極端に小さく、電圧も１．５Ｖ程度になるという。相対論の考察部分が間違っているならば、少なくともこの理論は間違いであろう。

　　（因みに、通常の相対性理論では、内部運動エネルギーの増加 �凾t は、エネルギーを担う担体粒子のみの運動量変化によって、�凾� ＝ �凾t/ｃ² にしたがってわずかに質量が増加する程度のものであり、ほとんど秤は変化しないはずである。たとえば、広島型原爆の全エネルギー放出による質量欠損は、わずか１（ｇ）である。

　　また、アキノ氏は、彼のＨＰの上部のマークよりおそらく”フリーメーソン”であり、ＨＰの下の方には”心理学と重力理論”というニューエイジ的な彼自身の論文が付けられているので、反キリスト的な惑わしに注意しなければならない。）

　　　　　　　　　　　　　　１．へ戻る